Un estadístico le echa un vistazo a su consumo eléctrico en tiempo real

I.

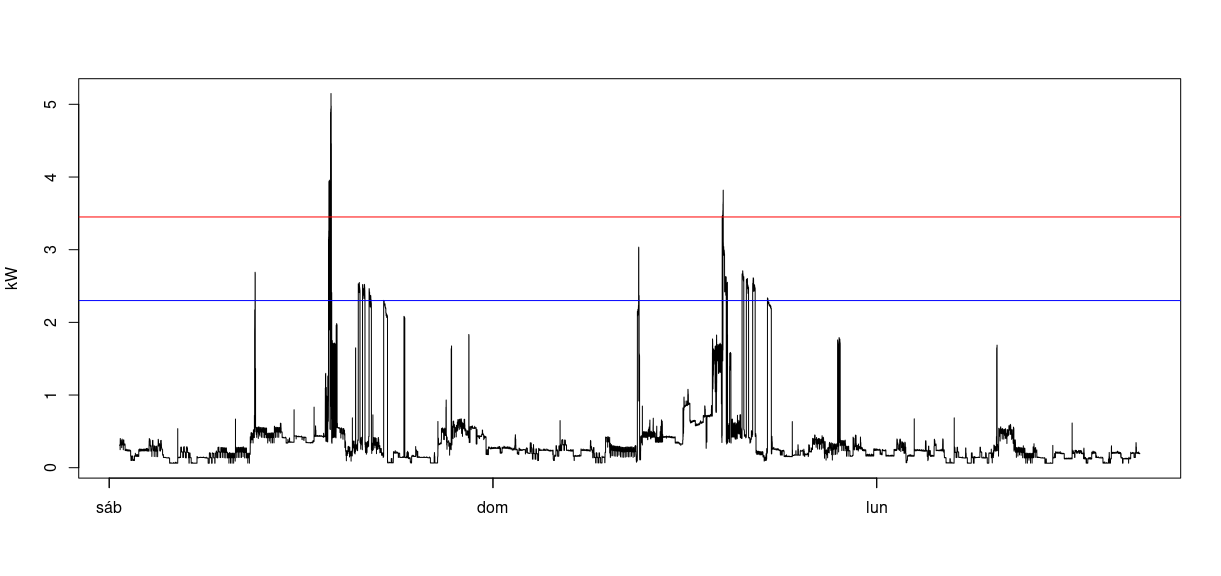
Por eso de que el Pisuerga pasa por Valladolid y que el diablo, cuando se aburre, mata moscas con el rabo, he instalado un cacharrito de 30 euros en el cuadro eléctrico de mi casa que mide el consumo (vatios, amperios y voltios)en tiempo real. En concreto, guardo medidas cada seis segundos aproximadamente. Mi perfil de consumo (potencia, en kW), sobre el que volveré luego, es así:

II.

En esto de la electricidad doméstica existen tres potencias —$P_r$, $P_c$ y $P_i$— que, en situaciones normales, cumplen la regla

$$P_r \le P_c < P_i.$$

$P_r$ es la potencia real, la de la línea negra en el gráfico anterior.

$P_i$ es la potencia máxima que da de sí la instalación eléctrica por el grosor de los cables, etc. Si se alcanza, por seguridad, sucede eso que antes se llamaba saltar los plomos y ahora se dice mangnetonosequé. Además, esos límites operan tanto globalmente —se puede ir la luz de la casa— como por circuito —podría saltar solo el de la cocina, etc.—.

El más jugoso es $P_c$, que es el de la potencia contratada. Si uno contrata, por ejemplo, como yo, 3.3 kW tiene realmente 3.45 kW (sí, en ciertos ámbitos, 3.3 = 3.45). Esa es la línea roja que aparece en el gráfico (y la línea azul corresponde a la otra potencia popular, la de 2.2 kW, creo). Al contratar 3.3 kW, la compañía eléctrica se compromete a proveerte de hasta 3.45 kW por un módico precio de unos 16 céntimos por kW y día (es decir, medio euro al día en mi caso). Tal es el precio del milagro cotidiano de que se encienda una luz al pulsar un interruptor.

III.

La teoría —en primera aproximación— dice que si $P_r > P_c$, se corta la luz. Pero como se ve en la gráfica anterior, los macarrones del sábado llevaron el consumo por encima de los 5 kW durante nueve minutos.

De hecho, es complicado no exceder los 3.45 kW habida cuenta de que la vitrocerámica consume casi 2 kW; la cafetera 1 kW; el microondas, casi otro; el lavavajillas, 1.5 kW —aunque no durante todo el ciclo de lavado—; etc. Apenas enchufas simultáneamente dos o tres cacharros que ocupan, calientan o hacen mucho ruido, rebasas los 3.45. Por eso, el interruptor de $P_c$, IPC para los disléxicos, tiene cierta tolerancia.

¿Cuánta? Es tema de enconado debate rodeado de cifras míticas. Un ejemplo más de cómo se comporta la masa anumérica enfrentada a curvas no lineales. Otros casos paradigmáticos en los que las respuestas de la plebe son parecidas tienen que ver con los logaritmos y los tipos del IRPF. En este caso en concreto, aparentemente, las tolerancias vienen indicadas por la curva gorda

(sí: parece que las tolerancias tienen tolerancias) extraída de la llamada norma UNE que, al parecer, está vigente.

IV.

No sé bien por qué he dejado todo esto escrito por aquí: tiene que ver solo marginalmente con lo que suelo tratar. Pero creo que a quien lo lea con atención le resonarán temas de relevancia estadística como el de la forma de la distribución del consumo, la naturaleza estadística de $P_c$, el problema de detección del uso de electrodomésticos por el perfil de consumo, la cuenta de cuánto habría que almacenar y cómo para aplanar la curva y pasar de una tarifa de 3.45 kW a una inferior (y si compensa), etc. O tal vez no. En todo caso, ahí queda.

Coda

El concepto de curva gorda hace referencia al afamado teorema del punto gordo.