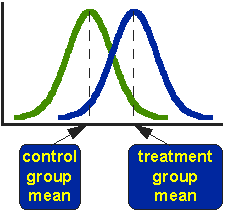
La paradoja (de Simpson) detrás de ciertos argumentos en pro de una subida generalizada de salarios
Trae El Confidencial un artículo de Javier Jorrín —según Jesús Fernández-Villaverde, el mejor periodista económico ahora mismo en España—, titulado La mejora de la productividad permitirá a las empresas prolongar la subida de salarios. El artículo se resume en tres enunciados que, así, en frío, según se verá, son contradictorios:
- Ha aumentado la productividad (PIB por hora trabajadda) en España.
- Eso da margen para que suban los salarios.
- El incremento de la productividad se debe a que ganan peso los sectores económicos más productivos.
La problemática relación entre (1) y (2) se la dejo a los economistas. Se pueden elaborar experimentos mentales en los que (2) se sigue de (1) y otros en los que no. Evaluar su pertinencia no es materia de estas páginas.